通过阅读该文,我认为你将收获什么:
- 你会知道微架构层面上矩阵乘法的优化方法
- 得到实现高性能CPU算法的一些思路
- 了解rust高性能编程相关的细节
- 接轨rust深度学习框架课程内容
了解一些微架构内容
了解一些基本名词:
- Word: 内存中的最小可寻址单元
矩阵乘法微架构优化思路
我们将目光放在矩阵乘分解后的微内核gebp上
这些优化思路的理论部分可以去看两篇论文:
将优化算法落地,代码成果如下:
矩阵乘算法在微架构上的可视化:
待补充
packed buffer
打包内存段,最主要的目的就是:
分块矩阵/子矩阵中的元素并不是连续的内存段。因此进行索引的过程比最小的TLB通道要大。解决方案是将分块矩阵打包到一段连续的内存中
micro-kernel
所谓的微内核,可以这样理解,矩阵size小的时候gemm性能很好,因为内存读写的压力很小,当size大了,性能会降低。实现一个kernel使得,这个规定尺寸下的gemm有很好的性能,将任意问题规模下的gemm分解成多个微内核的执行。该方法使得峰值性能得以维持,实现上,需要两步:
- blocking
- execute kernel
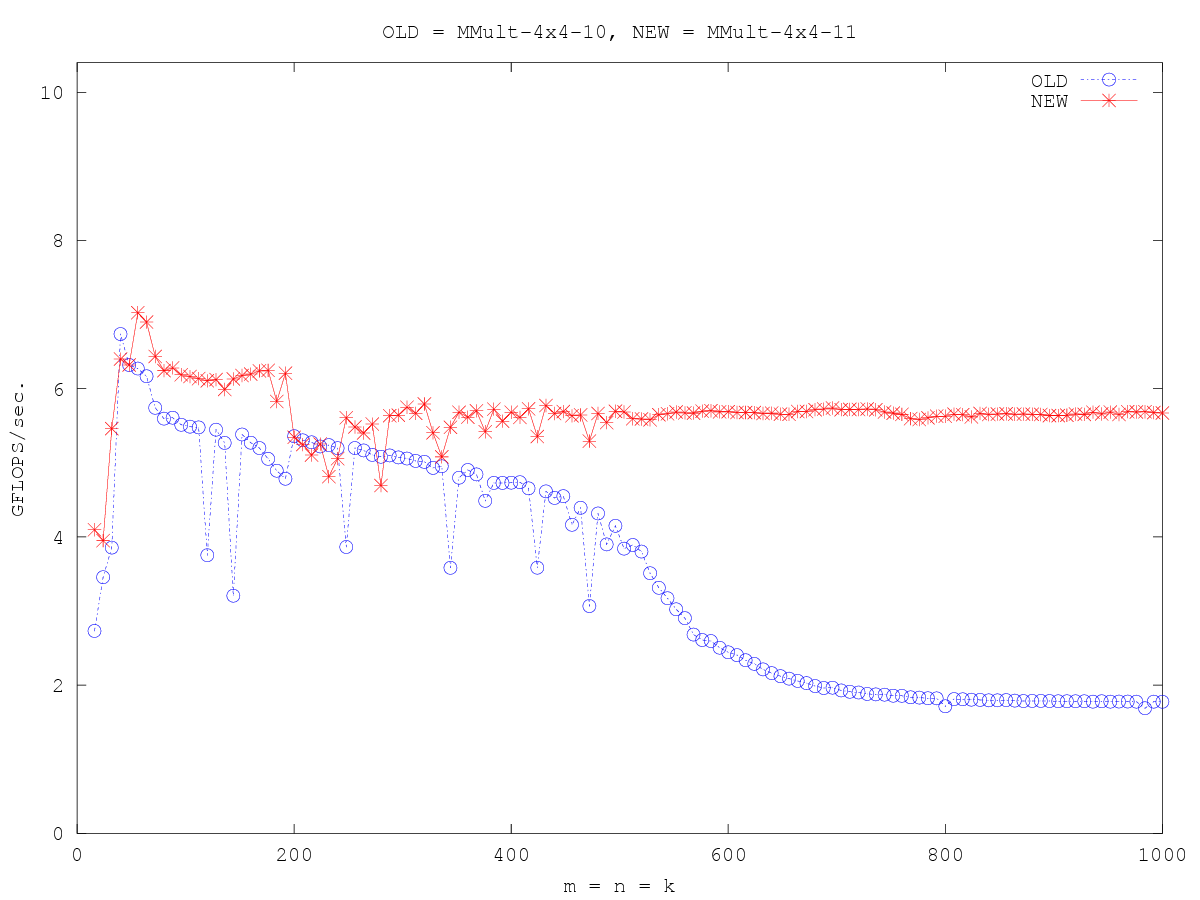
上面的benchmark:
https://github.com/flame/how-to-optimize-gemm/wiki/Optimization_4x4_11
如何blocking
分块的目的是让循环中复用的数据能够被放在更高速的存储单元上。
在论文Anatomy of High-Performance Matrix Multiplication中,分块顺序(可以理解为循环的顺序)为(文字描述配合图片一起看比较直观):
- 将B,C按列进行分块,分块之后,B和C变成了一条条的column panels,宽度为$n_c$
- 紧接着,A被分块成column panels,而B的column panels们再次被分块,变成row panels,两类panels的宽度都是$k_c$,与此同时,将$B$子矩阵进行打包,被打包的B将被安排到L3 cache中
- 这时候再对A的column panels进行分块,变成一个个block,其纵向长度为$mc$,横向长度则是上一个循环中的$k_c$,这时候将该block置入L2缓存
- 后面的两个循环放在一起说,因为他们共同构成了最终C的小块,A再次以$m_r$为步长在纵向上被分长了一个个小块$m_r * k_c$,而B则是被分成$k_c * n_r$的小块(这个小块在L1 cache上),最后再执行具有硬件亲和性的micro kernel,将其结果和现在的C小块不断相加即可,注意,C小块在寄存器上
下图为ndarray作者画的图
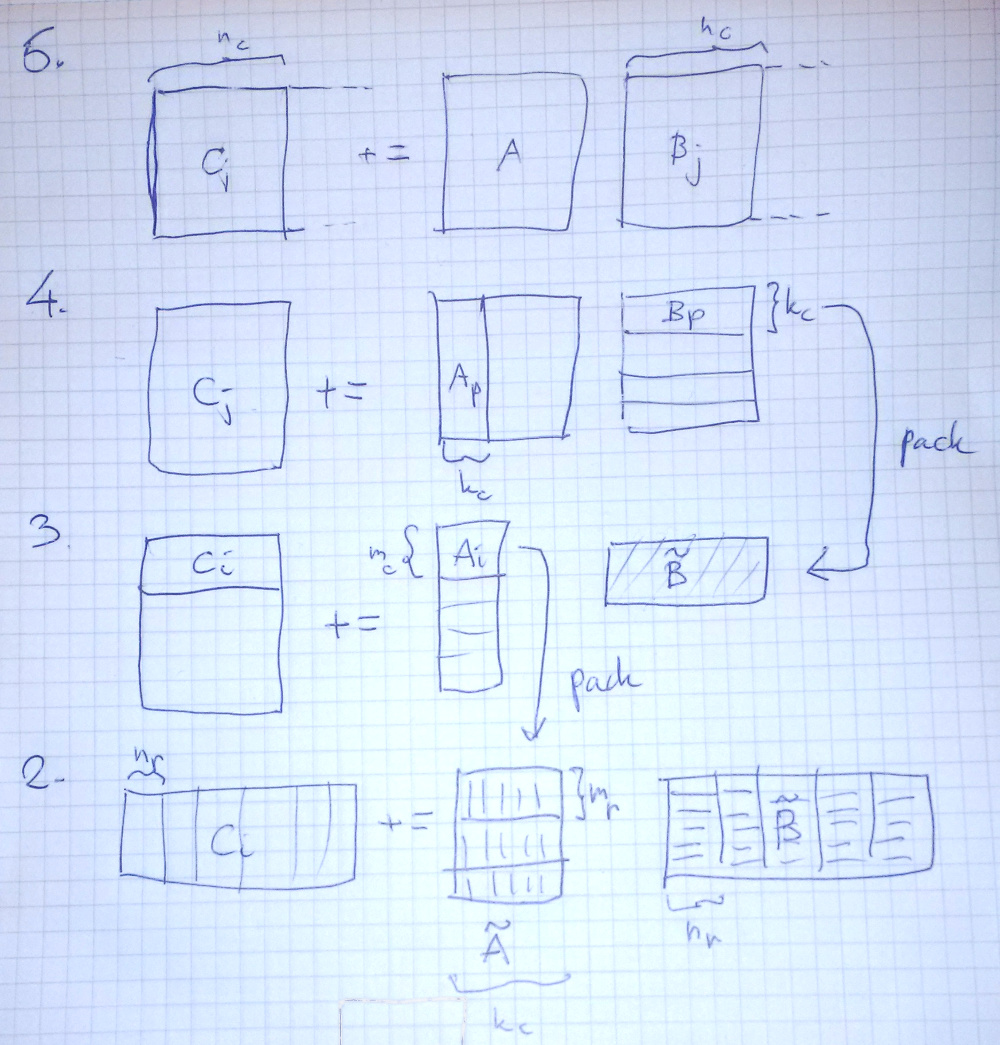
论文提出者的配图(老实说我觉得ndarray作者的涂鸦更加直观(狗头))
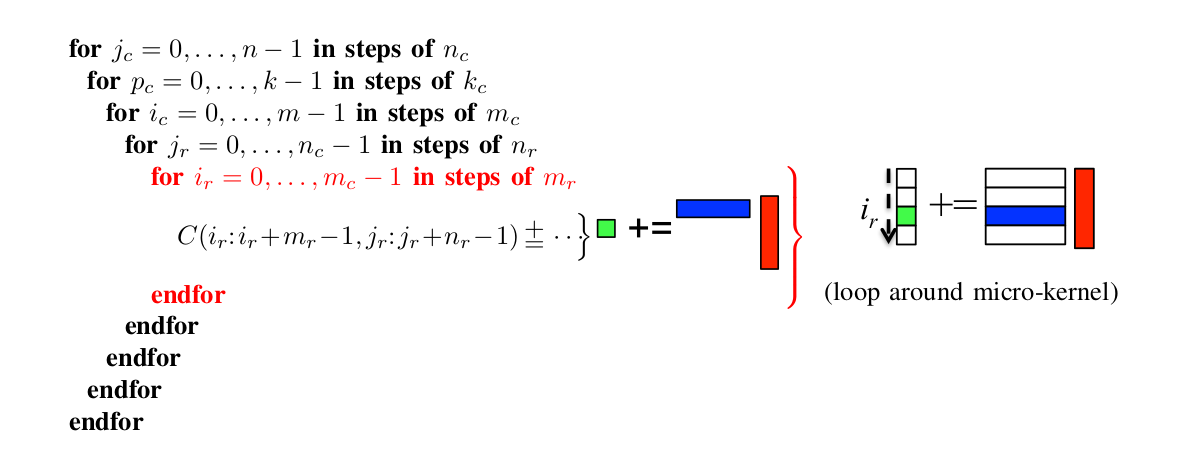
另外,我们应该也留意下存储层级的安排,这是高性能的关键:
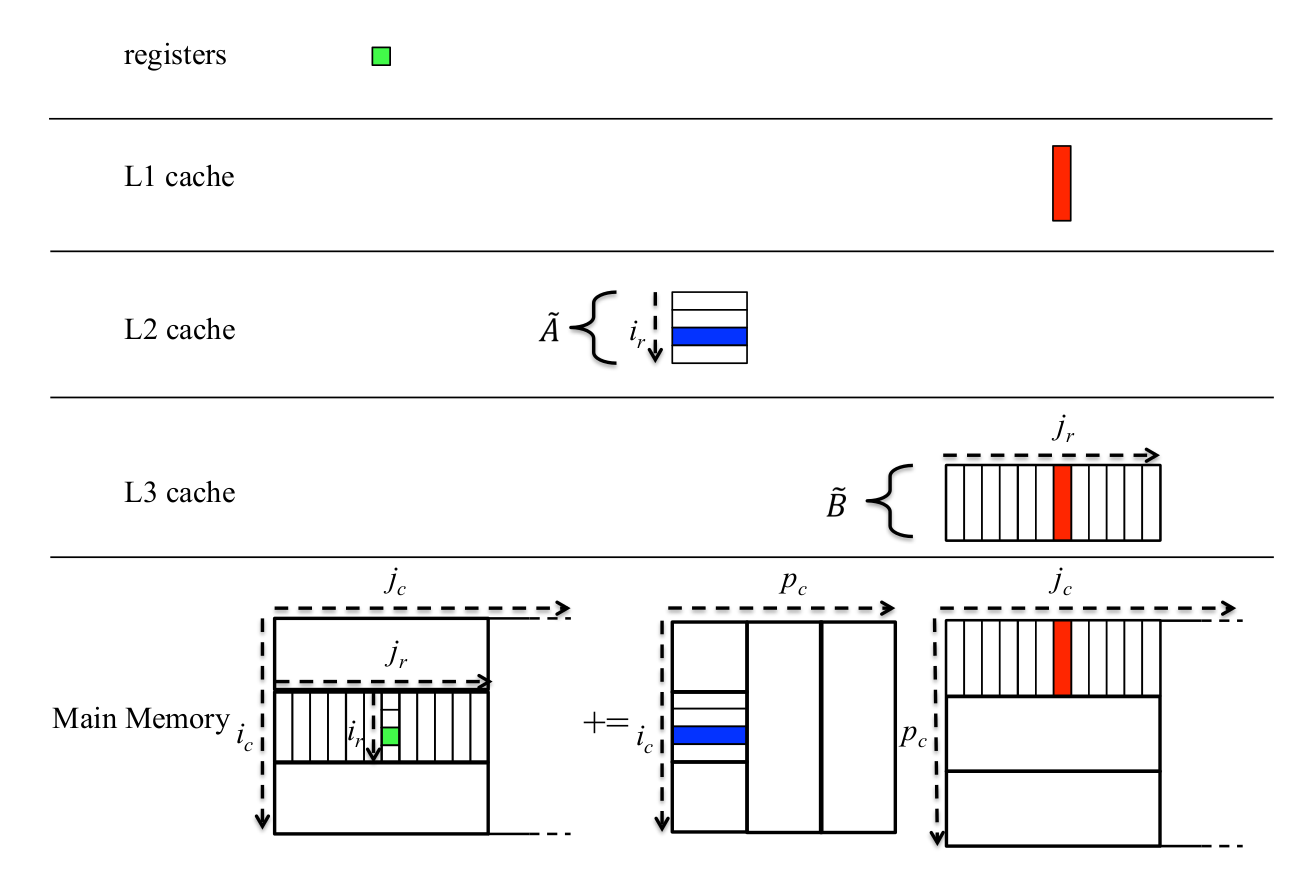
为什么这样blocking
回顾一下上文微架构内容中的部分以及上文提到的GOTOBLAS的最终方案,现在的情况是,通过看论文和开源实现,我们有了一个实践层面上优化的特别好的算法,这就好像知道了是一道题的标准答案,但问题是我还不知道这为什么会是标准答案,因此这一节我们就来讨论这个问题。
我们先梳理一下当前存在的问题:
- 是否可以以及如何将GEMM分解过程进行归类,依据是什么
- 为何要像上图中那样去进行CPU缓存与主存的分配
- 实现的程序中如何完成那样的分配
查阅论文的5.6 discussion,围绕着六种算法变体进行了讨论。
首先,一共有6种值得讨论的分块方法,它们的分解关系如下(图略丑,简单看看就好,详情还是看论文):
graph TD
A[GEMM]--> B1(GEPP)
A[GEMM]--> B2(GEMP)
A[GEMM]--> B3(GEPM)
B1[GEPP]--> C1(GEBP)
B1[GEPP]--> C2(GEPB)
B2(GEMP)--> C2(GEPB)
B2(GEMP)--> C3(GEPDOT)
B3(GEPM)--> C3(GEPDOT)
B3(GEPM)--> C1(GEBP)到这里我有一些迷惑,虽然论文给出了明确的分解方法,但我不明白为何要这样分,依据是什么
因此我去了解了一些可能相关的背景知识(核心论文的INTRODUCTION部分提到的参考文献):
看完论文后,我总结了一下理解论文的两个“口诀”来理解GEMM家族:抓住不变形和对称性
所谓不变性,是指对于原矩阵亦或是分块的矩阵,其组成部分的基本公式都是
$$C = A * B + C$$
对比论文中Algorithm中的伪代码,看出实际是数据复用对象的区别(即哪个对象被优先拷贝到上一层级中来完成计算)
优秀性能的关键在于这几个点:
- L2 cache的最佳带宽:这意味着需要首先排除GEPDOT-based实现(下图):
- s
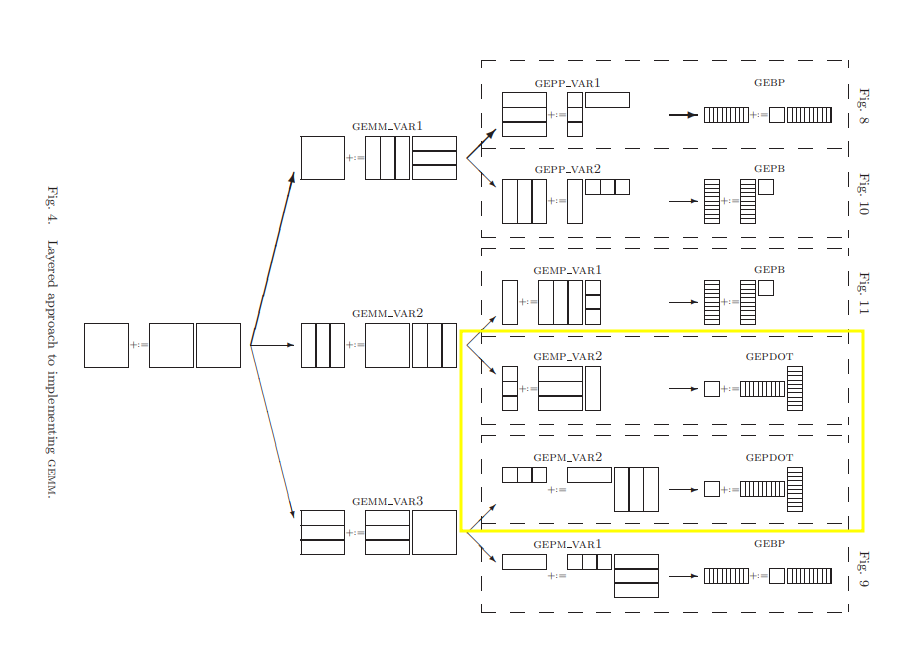
GOTOBLAS所采用的通过GEBP实现GEPP将$\tilde{A}$的尺寸都最大化了,通过将GFMM分解为GEPP_VAR1,
读者希望对上面的gemm_loop过程进行更详细的拆解和审阅,可以看(这些材料中所使用的符号是一致的)
- 论文Anatomy of High-Performance Many-Threaded Matrix Multiplication第二小结BLIS
- rust高效gemm开源实现MatrixMultiply库(Ndarray和Nalgebra)依赖的实现,文件名gemm.rs,函数为gemm_loop