Succinct Data Structures
引导
我们如何编码一个具体的的组合对象(例如树),使得即使用一个静态的占用很小内存的数据结构,仍可在恒定的时间内执行查询?
这里有一个问题,“占用很小”该如何定义?
按照维基百科的定义:使用的空间接近于信息论的下限值。
这种数据结构,不是“压缩表示”,允许高效的查询操作。
假设$Z$是存储某种数据类型的信息论最优数值,其表示可以有三种数据结构类型:
- implicit if it takes $Z + O(1)$ bits of space,
- succinct if it takes
bits of space, and
- compact if it takes
bits of space.
一些简洁数据结构的例子:
- bitvector
- tree;treap
- text collection
- Permutations
一个简单的例子:boolean array
该系列会包含的内容
- 理论基础, 推导(简单的)
- 可以参考的代码实现
- Rust(数据结构实现)
- Python(一些计算的估计,manim动画脚本)
《简洁数据结构》,数据结构的信息论下界
- 引导部分
- “惊喜程度”与“熵”的直观理解
- Worst-Case Entropy
- Shannon Entropy
《简洁数据结构》,bit vector的构成与表示(Rust实现)
- bit vector的API介绍
- bit vector的Query动画
- 位向量表示&Rust代码介绍
《简洁数据结构》,array抽象以及部分和的应用
《简洁数据结构》,bit vector的Rank效率优化
《简洁数据结构》,bit vector的Query优化以及应用场景
《简洁数据结构》,
什么是Compact data structure
参考资料
- 书本Compact Data Structure
- https://web.stanford.edu/class/archive/cs/cs166/cs166.1226/
- https://stackoverflow.com/questions/72580828/what-is-a-succinct-rank-data-structure-how-does-it-work
概览
一个例子:static bounded subset
我们要研究几个问题:
- 什么是Succinct Data Structures
- 什么是Succinct Index
- rank和select的时间复杂度如何优化
- 简洁数据结构如何应用在实践中,需要一个具体的例子
简洁数据结构简而言之就是:
简洁的数据表示 + 简洁的索引
Succinct Index,为数据结构赋能,使其完成高效查询的辅助的简洁表示,其空间复杂度必须满足:$o(LogL)$
以及我们最终的目的是,使其满足和理论值一致的查询时间复杂度
至于后面的问题,我们在具体的实现章节回答
理论&估计
我们假设数据结构的输入来源于L个不同源头。那么使用输入表示的数据一定会使用:
$ceil(LogL)+o(logL)$bits
至于信息论的下界为何是这个值,可以参考数据结构的信息论下界推导
Query
对于紧凑的数据结构来说,Rank和Select都是最重要的两种query操作,为何如此?
一开始我对这个问题的答案非常好奇,找到很多的相关博客以及一些高阶课程课件以及论文,但这些都没有回答我的问题,直到我阅读了一本和数据压缩以及字符串处理领域的大牛Gonzalo Navarro所写的Compact Data Structure,情况才有所好转。
这个问题背后最根本的问题实际是“对于紧凑的数据表示,索引在实际场景中的表现主要是什么?”
我们现将目光放到两个关键的场景:
- 文本压缩
Arrays
一个数组 $A[1, n]$ 是一个元素序列,可以在任意位置进行读取和写入。也就是说,数组是一种抽象数据类型,支持以下操作:
- read(A, i):返回 A[i],对于任意 1 ≤ i ≤ n
- write(A, i, x):设置 A[i] ← x,对于任意 1 ≤ i ≤ n 和任意 x。
与经典的数组编程结构不同,我们对空间高效的数组表示感兴趣,这些表示希望能够只存储每个数字 A[i] 的有用位。在某些情况下,数组的值是统一的,使用相同数量的位来存储所有元素是合理的。在其他情况下,数字之间的差异很大,我们更倾向于为每个元素分配可变数量的位。
元素为固定大小的数组

元素为可变大小的数组
bit vectors
API
位向量及其操作是简洁数据结构的基础
设 $S \subseteq {0, 1, \ldots, u - 1} $ 是一个位向量中设置位的位置集合,其中位向量长度为 $u$。我们的位向量支持以下查询:
- Access(i) 返回
true如果i在S中,否则返回false - **Rank(i)**返回 $ alpha \in S | \alpha < i \ $ 的基数
- Select(k) 返回S中第k个i
- Update(i) 向S中插入或删除z
这里存在一个问题就是,Bool数据类型理论上只需要用1bit存储,为何诸如C,Rust等语言中的bool类型的数据所占内存空间都是1byte呢?非常简单:
因为大多数CPU芯片都依照byte进行寻址
因此实现一个bit_vector,一定是需要用一些技巧的(位运算)
简单地去证明这件事,来看:
pub struct BitVector {
words: Vec<usize>,
len: usize,
}usize的大小取决了系统位数,相信大部分人用的开发机都是64位的,那么usize的内存占用空间便是8字节,即64比特
len就是bit vector的长度:注意,不是words的长度
如何表达
那么这个结构该如何表达一个具体的bit vector呢?
首先是用该结构体表示的对象一定能够和理想化的bit vector对象形成双射,简单地证明一下:
首先需要清楚usize类型可以表达任意一个64位的位向量,这很容易理解:二进制和十进制系统中的符合构成双射,当需要表达的位数超过64,只需要再往vec<usize>中增加一个新的元素就好了,这样看,len是不是显得没有必要?不是的,试想如果没有len,表达[1, 1]该咋表达,如果单用words = [2],实际表达的是$[0,0...1,1]$,其中0有62个这和需要的并不一致。
现在,再来看看空间的问题,我们假设需要表达的位向量长度位$n$,则该数据结构占用的内存也是近似于$n _{bit}$
Access/Read
访问bit_vector的第i个元素
由“如何表达”章节,我们对于bit_vector是如何实现的,已经有了较清晰的认识,那么现在我希望得到第i位元素,实现也很容易就能得到:
// 显然64位系统上,WORD_LEN的
pub const WORD_LEN: usize = std::mem::size_of::<usize>() * 8;
fn access(&self, pos: usize) -> Option<bool> {
if pos < self.len {
let (block, shift) = (pos / WORD_LEN, pos % WORD_LEN);
Some((self.words[block] >> shift) & 1 == 1)
} else {
// 越界的时候,返回空值
None
}
}值得注意的代码应该是:
(self.words[block] >> shift) & 1 == 1self.words[block]得到的是pos所"被包含"的usize变量,shift代表在指定usize变量所代表的二进制变量的偏移量。
一个例子,假设self.words[block]是$2^{62} + 2^{63}$即$13835058055282163712$,而pos为$n * 64 + 62, n \in \mathbb{N}$
则经过右移操作后,得到的数值为3(十进制),最关键的是通过$and$操作符,我们能得到其第一位(即我们的i所指向的位)是否为1
这里有一个问题是,如何得到一个切片的值(如"01001101"中的最后三位"101")
形式化表达
Compact Data Structure书中给到了相应的形式化表述:
In general, we will assume that the elements use a small number of bits, which fit in a computer word of w bits and thus can be manipulated in constant time. We call “integer” the numeric data type offered by the language using w bits
上述是对Words的描述
首先书中提到的获取$B[j]$的方法如下:

对于bit array,我们有:
这里$B[j] = {\lfloor W[j]/2^{w-j} \rfloor} mod 2$
实际上这是因为: $$ n >> k = \lfloor n/2^k \rfloor $$
验证代码可以使用:
tem = 2173192
bin_tem = bin(tem)
# 用于验证公式是否可用:print(bin_tem)
# 获取一个数字的二进制表示的总位数
def words(j):
return len(bin(t)) - 2
# 返回数字的二进制表示第j位的值
def get_bit_dec(dec, j):
return int(k/2 ** (words(k) - j)) % 2update(动态结构)
待填坑
Rank
该API可以理解为前n项和
首先,先不考虑words中最后一个元素的的值是多少,对于前几个word,我们要有一个函数,可以计算出usize的二进制表示中非零之和,这类函数一般称popcount,rust标准库中的usize具备count_ones方法可以为我们完成相应计算
#[inline(always)]
pub const fn popcount(x: usize) -> usize {
x.count_ones() as usize
}至于最后一个usize对象,我们联想到Access中右移的方法可以得到该块中的指定索引位之后的比特位,反过来,我们左移64-偏移量即可获得一个包含同样Rank的usize变量,对其使用popcount再将前面块的数加在一起,就是结果了:
fn rank(&self, pos: usize) -> Option<usize> {
if self.len() < pos {
return None;
}
let mut r = 0;
let (wpos, left) = (pos / WORD_LEN, pos % WORD_LEN);
for &w in &self.words[..wpos] {
r += popcount(w);
}
if left != 0 {
r += popcount(self.words[wpos] << (WORD_LEN - left));
}
Some(r)
}该算法非常直观,其算法复杂度也容易评估,显然和bit_vector的长度呈线性关系(words的长度和bit_vector呈比例关系),因此算法复杂度是$O(u)$
那么一个问题是,有没有办法优化呢?
优化思路探索
多级前缀和(Multilevel Prefix Sums)
能想到的最简单的方法一定是用一张表来保存前N项的rank值,即prefix sum
假设bit_vector的长度为$n$,则rank值最大为$ceil(lg(n))$
比如1023位,则$2^{10}=1024$,因此10bit的存储类型能够覆盖该bv的需要,那么我们可以得到存储开销为:$O(nlogn)$,此时rank的时间复杂度达到了$O(1)$
沿着这个思路,想要进一步缩小存储开销,可以将查询的结构分块,我们后面将查询的数据结构称为ps(prefix sum),我们假设块的大小为$b$,那么这时$rank(i)$的计算方法就转换为了:
- 读取第$\lfloor{i/b}\rfloor$位ps的值
- 扫描并求第$\lfloor{i/b}\rfloorb$到$\lfloor{i/b}\rfloorb + i\mod b - 1$的和
从而空间复杂度转为$O({\frac{nlogn}{b}})$,但代价是查询效率变成了$O(b)$
查询效率到了$O(b)$可就不简洁了,因此我们再结合prefix,但这时候上限变小了,因为我们有了块的概念,从而我们可以将上述算法的第二部求和的的数值变小,即:
$O({\frac{nlogn}{b}} + nlogb)$,这时候rank的时间复杂度就再次变成$O(1)$
到这一步,自我感觉非常良好了(Flag, -_-||),其实还存在着一个问题:有$b$数吗? -> 如何设置$b$
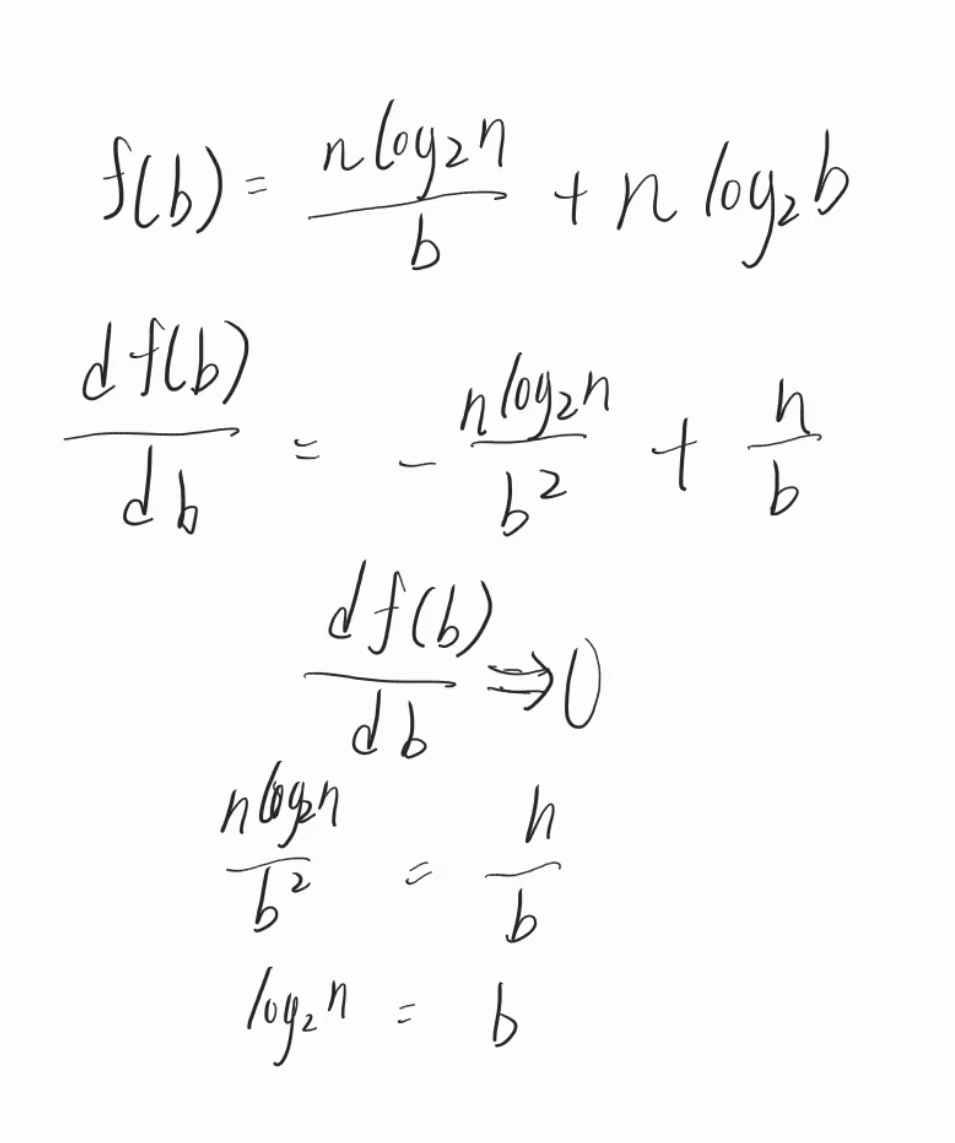
从而空间占用可以被优化为$O(nloglogn)$,对于一个块,我们会有和bit vector等长的结构用于存储其块级别的rank,我们称每一个块的rank为block-level rank
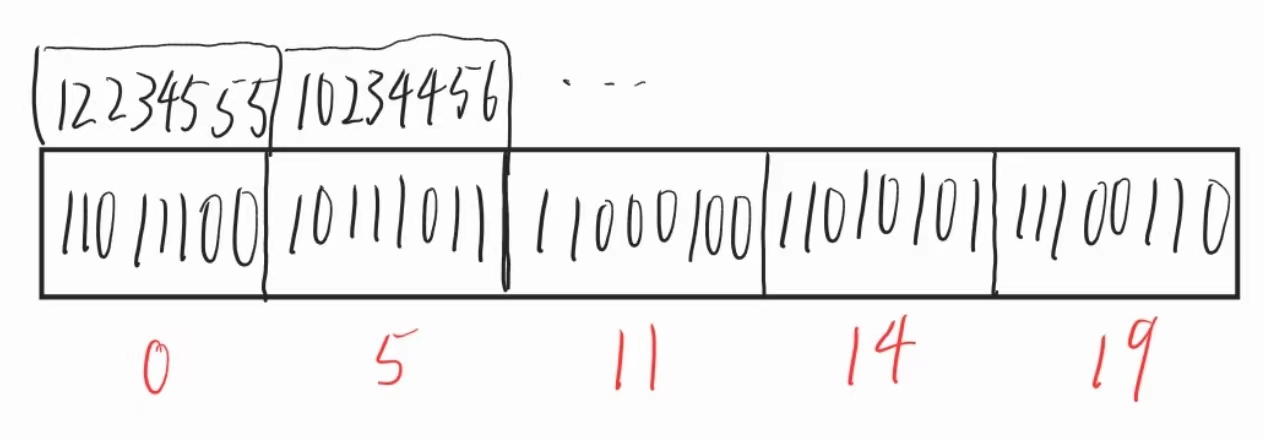
我们注意到,上述优化过程可以不断地进行下去,因为每个block都可以再被划分为嵌套的sub-block,我们用$log^{k}n$代表对n使用k次对数函数,通过不断分解block,我们可以:
$O({\frac{nlogn}{b}} + nloglogb) \overset{b=logn}{\rightarrow} n + log^{3}n = O(nlog^3n)$
如图:
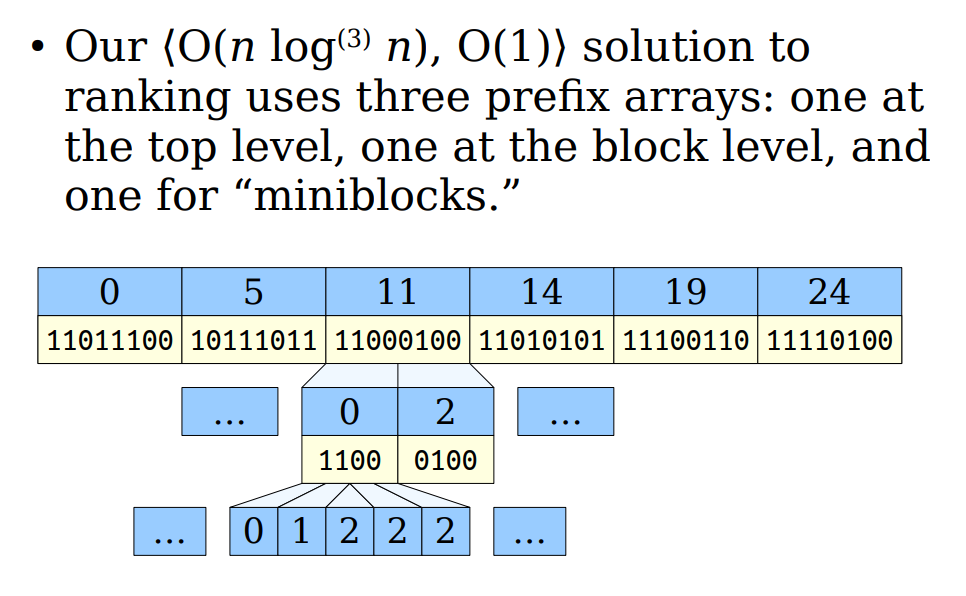
注意到,从上图的由上至下的结构中,我们需要用到$k-1$层存储nbit的结构,以及最后一层会使用到$nlog^kn$ bit,而我们的查询时间复杂度变成了$O(k)$
凭直觉,$k$是存在上界的,但是对于非常大的bit_vector来说,这个值的上界应该非常大,而$log^k$函数本身缩放能力极强,对于任意自然数$n$,总能找到一个$k$值使得$log^k n \leq 2$,其中最小的k值所构成的迭代对数函数便是$log^*n$,从而我们发现:当n固定下来,我们一定能得到一个$<O(nlog^*n), O(log^*n)>$的方法来进行rank,前者为空间复杂度,后者为时间复杂度,这个方案叫Multilevel Prefix Sums
Four Russians

这里需要弄清楚的是两件事:
- 如何对b-block进行拆分
- 什么是Four Russians
这里第一个和第二个问题实际上是强关联的,进行拆分的大小要满足使用Four Russians的约束。进行拆分后,b的值确定,那么可能的数量实际是$2^b$个(图中的列),而行则是$b+1$,同前面一样,表中的每个格子的大小实际为$logb$,因此对于一个子块,开销为$O(2^b * b * logb)$,如何使得该值最小呢?
这里我们得对b进行一个估计,我们假设b为$\frac{logn}{2}$,
混合方法
Darray结构
Darray是dense array的简称,这个结构体需要组合两个内嵌结构,分别是DArrayIndex和Rank9SelIndex
pub struct DArrayIndex {
block_inventory: Vec<isize>,
subblock_inventory: Vec<u16>,
overflow_positions: Vec<usize>,
num_positions: usize,
over_one: bool,
}
pub struct Rank9SelIndex {
len: usize,
block_rank_pairs: Vec<usize>,
select1_hints: Option<Vec<usize>>,
select0_hints: Option<Vec<usize>>,
}
pub struct DArray {
bv: BitVector,
s1: DArrayIndex,
s0: Option<DArrayIndex>,
r9: Option<Rank9SelIndex>,
}Rank9SelIndex这个结构体(后文简称r9),就是用于辅助bit_vector提供更高速的rank算法的。因此r9的构造依赖于bit vector实例。
关于Rank9算法的实现原理,可以参考https://vigna.di.unimi.it/ftp/papers/Broadword.pdf
const BLOCK_LEN: usize = 8;
fn build_rank(bv: &BitVector) -> Self {
let mut next_rank = 0;
let mut cur_subrank = 0;
let mut subranks = 0;
let mut block_rank_pairs = vec![next_rank];
for i in 0..bv.num_words() {
let word_pop = popcount(bv.words()[i]);
let shift = i % BLOCK_LEN;
if shift != 0 {
subranks <<= 9;
subranks |= cur_subrank;
}
next_rank += word_pop;
cur_subrank += word_pop;
if shift == BLOCK_LEN - 1 {
block_rank_pairs.push(subranks);
block_rank_pairs.push(next_rank);
subranks = 0;
cur_subrank = 0;
}
}
let left = BLOCK_LEN - (bv.num_words() % BLOCK_LEN);
for _ in 0..left {
subranks <<= 9;
subranks |= cur_subrank;
}
block_rank_pairs.push(subranks);
if bv.num_words() % BLOCK_LEN != 0 {
block_rank_pairs.push(next_rank);
block_rank_pairs.push(0);
}
block_rank_pairs.shrink_to_fit();
Self {
len: bv.num_bits(),
block_rank_pairs,
select1_hints: None,
select0_hints: None,
}
}应用场景
一个直接点的问题:实现了bit vector这个数据结构,它在什么情况下能够派上用场呢?